 |
 |
Arbeitsgruppe Diskrete Optimierung |
TRAVELING SALESMAN PROBLEM
Aufgabe
- Klassische Problemformulierung: Ein Handelsreisender möchte eine Rundreise durch vorgegebene Städte machen (oberes Bild). Jede Stadt soll genau einmal besucht werden. In welcher Reihenfolge soll er die Städte besuchen, um möglichst schnell oder kostenminimal wieder zu Hause zu sein?
- Abstrakte Problemformulierung: Finde einen kürzesten Hamiltonschen Kreis in einem gewichteten Graphen.
Anwendungen
- Fahrtroutenoptimierung durch vorgegebene Orte (siehe Deutschlandkarte rechts).
- Leiterplattenfertigung in der Elektrotechnik (mittleres Bild): Bohrlöcher oder Bauelementepositionen entsprechen Städten. Bewegungszeiten eines Roboterarmes entsprechen Reisezeiten zwischen Städten.
- Röntgenkristallographie: Ein Kristall wird in verschiedenen Positionen bestrahlt. Aus Röntgenbildern wird auf Kristallstruktur geschlossen. Kristallpositionen entsprechen Städten, Zeit zum Wechsel zwischen zwei Positionen entspricht Reisezeit zwischen zwei Städten. Minimiere Experimentzeit.
- Gasturbinenwartung von Flugzeugen: dort treten spezielle Traveling Salesman Probleme auf.
- Lagerhaltung: Ein Fahrzeug soll in einem Lager alle Teile eines eingegangenen Auftrags sammeln. Die Standorte der Teile entsprechen den Städten. Fahrzeugbewegungszeiten entsprechen Reisezeiten.
- Verdrahtungsprobleme in Computersystemen: es gibt Spezialfälle bei denen genau zwei Leitungen an einen Kontaktpunkt angelegt werden. Minimiere die benötigte Leitungslänge mittels eines TSPs.
- Produktionsplanung: Verschiedene Teile sollen auf einer Maschine gefertigt werden. Dazu muss die Maschine mehrmals umgerüstet werden. Zustände der Maschine entsprechen Städten, Umrüstzeiten entsprechen Reisezeiten. Minimiere Gesamtumrüstzeit.
- Astronomie: Eine Sternwarte soll an 1 Million Sternen eine Messung durchführen. Das Anvisieren der Sterne kostet Zeit. Sterne entsprechen Städten, Wechselzeit von einem Stern zum anderen entspricht Reisezeit. Minimiere die teure Belegungszeit der Sternwarte.
- Gentechnik: Das TSP tritt als Hilfsproblem beim Zusammensetzen von Genteilsequenzen auf.
- Glasfasernetze: Minimiere die verlegte Glasfaserstrecke bei einer Ringtopologie des Netzwerks.
Problem
- Schwierigkeitsgrad: So einfach wie das Traveling Salesman Problem zu verstehen ist, so schwer ist es zu lösen. Die Komplexitätstheorie beweist: das TSP ist aus theoretischen Gründen ein extrem schweres kombinatorisches Optimierungsproblem (NP-schwer).
- Rechenintensität: Das Auffinden einer kürzesten Rundreise ist rechenzeitintensiv. Große Probleme (Bild unten) benötigen heute auf Parallelrechnern Jahre zur Lösung. Trotz moderner Hard- und Software.
Warum nimmt man von den endlich vielen Rundreisen nicht einfach eine kürzeste?
Ergebnis: "Durchprobieren" aller Rundreisen führt nicht zum Ziel. 100 Städte => mehr mögliche Rundreisen als Elementarteilchen im Weltall.Problemgröße: 50 Städte Anzahl der verschiedenen Rundreisen: etwa 3·1062 (eine Zahl mit 63 Stellen) Anzahl der Prozessoren (10 GHz): 1 Milliarde (massiver Parallelrechner) Berechnungszeit für alle Rundreiselängen: mindestens 9·1035 Jahre (36stellige Zahl)
Lösung
- Theorie: Guter Lösungssoftware gehen tiefgreifende theoretische Vorüberlegungen voraus (Algorithmen, polyedrische Untersuchungen).
- Software: Aufwendige Umsetzung moderner algorithmischer Ideen in komplexe Softwaresysteme.
- Verfahren: Schnittebenenverfahren, Verzweigungsverfahren, Branch-and-Cut, Heuristiken, effiziente kombinatorische Algorithmen und Datenstrukturen, Parallelrechner...
- Grenzen: Die Lösung eines 15112 Städte Problems bedeutet den vorläufigen Weltrekord (rechts); Probleme mit bis zu 1000 Städten können heute gut gelöst werden.
Methodentransfer
- Modellproblem: Das TSP wird oft als Modellproblem zum Test neuer Algorithmen und Ideen verwendet.
- Transfer: Am Modellproblem TSP gewonnene Erkenntnisse und Ideen werden auf andere schwere Optimierungsprobleme übertragen.
- Beispiele: Direkter Erkenntnistransfer zu Vehicle Routing Problemen (Optimierung von Fuhrparkeinsätzen), Sequential Ordering Problem (Reihenfolgeplanung, optimale Roboterauslastung), und zu vielen anderen kombinatorischen Optimierungsfragestellungen.
Ansprechpartner

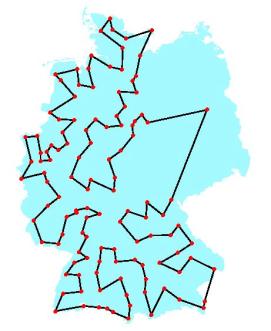
Kürzeste Rundreise durch 120 Städte
(Grötschel 1977)
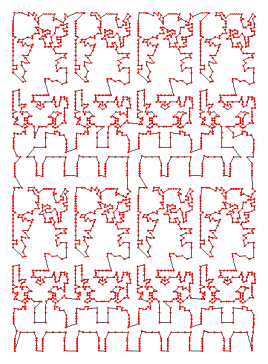
Leiterplatte mit 2392 Bohrungen
(Padberg und Rinaldi 1987)
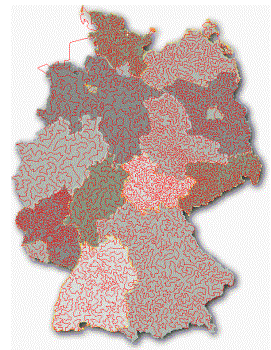
Kürzeste Tour durch 15112 Städte
(Applegate, Bixby, Chvátal, Cook 2001)