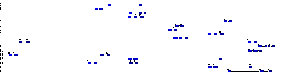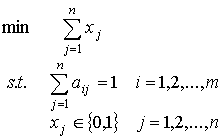![]()
Solution of Large Scale Crew
Scheduling Problems
Problem description
A set of basic activities or tasks – typically, to fly an aircraft
from A to B – has to be assigned to sets of crew members such that all basic
activities are covered. The basic activities are grouped into so-called pairings that are
sequences of tasks usually starting and ending at the same home base.
Additionally, complex rules and regulations coming from legislation and
contractual agreements have to be met by the solutions. These often cannot be
modelled as linear constraints.
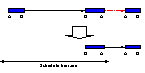
Fig. 1: Two among large number of feasible solutions of a small-sized crew scheduling problem. Mathematical
model
Let
The The number of feasible pairings can be several millions even for only medium-sized problems. Effcient methods have to be applied to attack such problems with a huge number of variables. ContactTran Van Hoai Im Neuenheimer Feld 368 |
Methods
·
Parallel Branch and Cut on the pure IP formulation with: o Strong cutting planes, such as: §
Clique inequalities: §
Odd cycle inequalities: o Preprocessing, such as: §
Eliminate duplicated columns, §
Eliminate dominated rows, §
Reduced cost fixing o Searching B&B tree in parallel with the master-slave model.
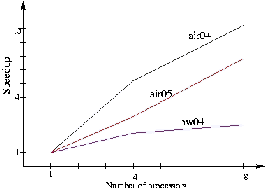
Fig. 2: performance of parallel branch and cut to solve small-sized crew
scheduling problems. ·
Branch and Price with: o Column generation method on flight network by solving: §
Constrained Shortest Path problems, §
K-Shortest Path problems with black-box rule
checking, §
Heuristic Enumeration o Column generation by Constraint Logic Programming, utilizing the propagation
of non-linear constraints on feasible region. ·
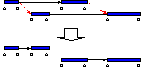
Local Search Heuristics to improve the solution,
(see Fig. 3)
Fig. 3: three local search heuristics to reduce cost function. |