Arbeitsgruppe Diskrete Optimierung

Kaktusdarstellung minimaler Schnitte

Kakteen

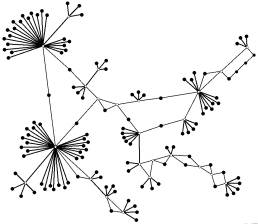
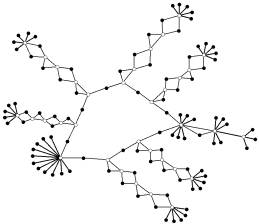
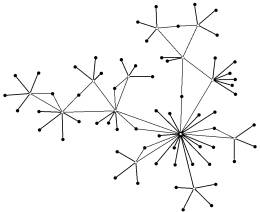
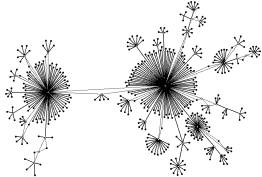
• Ein Kaktus ist ein Graph, in dem jede Kante in höchstens einem Kreis enthalten ist (siehe Beispiele rechts).
• Verwendbar als effiziente Datenstruktur zur Speicherung aller minimalen Schnitte eines Graphen.
• Kakteen können die minimalen Schnitte eines Graphen kompakt und strukturanzeigend speichern.
• Die Teilmengen- und Überlappungsstruktur der Menge aller minimalen Schnitte eines Graphen ist an einer Kaktusdarstellung dieser Menge ablesbar.

Motivation

• Kakteen spiegeln wesentliche Informationen wider, die in Zwischenergebnissen (gewichtete Graphen) bei der Lösung schwerer kombinatorischer Optimierungsprobleme anfallen (TSP, CVRP, usw.).
• Beschleunigung von Schnittebenenverfahren und des Branch-and-Cut Ansatzes für Ansatzes für derartige Probleme.
• Beobachtung, dass die Zwischenergebnisse bei bestimmten Optimierungsproblemen strukturelle Eigenschaften besitzen, die es erlauben die Kaktuskonstruktion wesentlich zu beschleunigen.
• Die Kaktusdatenstruktur ist eine Komponente in unserer Lösungssoftware für das TSP und das CVRP.

Beitrag

• Neue algorithmische Idee zur Konstruktion von Kaktusdarstellungen von minimalen Schnitten.
• Spezialisierung auf bestimmte Typen von Graphen welche im besonderen Interesse der Arbeitsgruppe liegen.
• Speicherplatzreduzierung : von bisher GBytes auf nun MBytes für relevante Poblemgrößen.
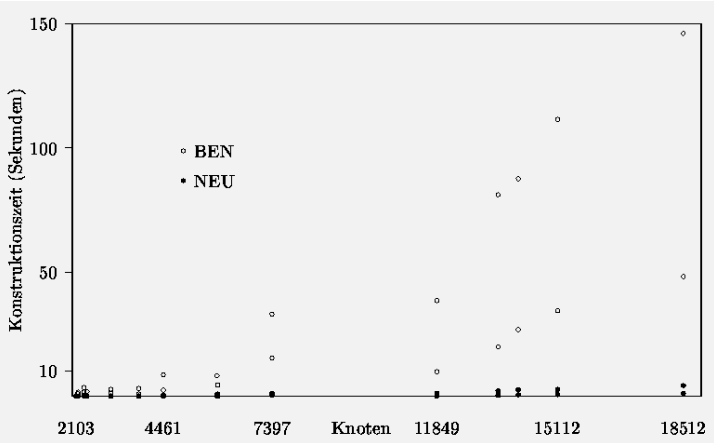
• Geschwindigkeitssteigerung: NEU ist der neue Algorithmus, BEN ein sehr guter Benchmarkalgorithmus.

Beispiel

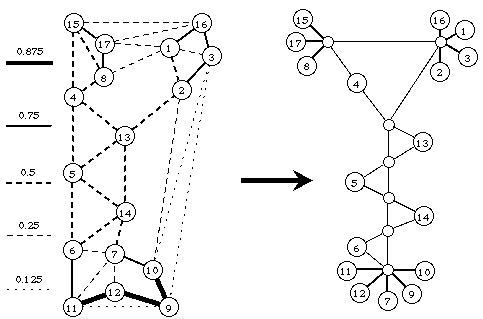
• Unten links ist ein sogenannter TSP Trägergraph G mit minimalem Schnittgewicht 2 abgebildet.
• Der zugehörige Kaktus (rechts) speichert alle minimalen Schnitte von G und zeigt deren Struktur.
• Entferne zwei Kanten eines Kreises im Kaktus oder entferne eine fette Kante, um den Kaktus zu zerlegen und zwei Minimalschnitte von G zu erhalten. Alle minimalen Schnitte von G können so erhalten werden.

Ansprechpartner