Physical Mapping Problem

Motivation Eine grundlegende Aufgabe in der Molekularbiologie ist die Analyse von menschlichen Chromosomen. Ein Chromosom besteht aus einer Aneinander-reihung von etwa 100 Millionen Basenpaaren. Eine Rekonstruktion dieser Reihenfolge direkt aus einem kompletten Chromosom ist zur Zeit nicht möglich. Daher ist es notwendig, den vollständigen DNA-Strang in kleinere Teile zu zerlegen und diese Fragmente einzeln zu untersuchen. Das Problem dabei ist aber, dass bei der Zerlegung Informationen über die An-ordnung der DNA-Fragmente (Clones) verloren gehen. Das Problem der Wieder-herstellung dieser Ordnung nennt man Physical Mapping. Vorgehensweise Eine mögliche Vorgehensweise beim Physical Mapping arbeitet mit sogenannten STSs (Sequence Tagged Sites), auch Probes genannt. Das sind DNA-Sequencen, die nur an einer einzigen Stelle des Chromosoms auftreten. Diese Probes können z.B. durch Extrahieren von DNA-Sequenzen aus den Enden der Clones gewonnen werden, in diesem Fall spricht man vom Physical Mapping Problem mit Endprobes. Mit Hilfe von Hybridisierungsexperimenten kann man zu jedem Probe-Clone-Paar feststellen, ob das Probe innerhalb der Clone-Sequenz liegt, oder nicht. Normalerweise hybridisiert das Probe mit dem Clone, falls es im Innern liegt, ansonsten nicht. Die Ergebnisse dieser Experimente lassen sich also als eine Matrix mit #Clones Zeilen und #Probes Spalten schreiben (#Clones bzw. #Probes steht dabei für Anzahl der Clones bzw. Probes). Die Einträge dieser Hybridisierungsmatrix sind 1 (in Abb. 1 und 2 ausgefüllt dargestellt), falls das entsprechende Testergebnis positiv ist (Probe und Clone hybridisieren) und 0 (in Abb. 1 und 2 nicht ausgefüllt dargestellt) bei einem negativen Ergebnis. Aus dieser Matrix soll nun die Anordnung der Clones im Chromosom rekonstruiert werden. Fehlerbehandlung Das wesentliche Problem bei dieser Rekonstruktion ist, dass die Hybridisierungsexperimente fehlerbehaftet sind. Zwei der Fehler, die typischerweise auftreten, sind zum einen die false-positive Fehler (eine Hybridi-sierung wird angezeigt, obwohl das Clone das Probe nicht enthält und zum anderen die false-negative Fehler (keine Hybridisierung wird angezeigt obwohl das Probe in Wirklichkeit innerhalb des Clone liegt). Ohne diese Fehler könnte das Physical Mapping Problem einfach auf das Lösen eines sogenannten Consecutive Ones Problem zurückgeführt werden. Will man aber die tatsächliche Anordnung der Probes trotz Fehler möglichst exakt bestimmen, so greift man auf die Idee der Maximum-Likelihood-Schätzung zurück. D.h. man versucht aus einer beobachteten Hybridisierungsmatrix die eigentliche Matrix (die im fehlerfreien Fall entstanden wäre) zu schätzen. Kennt man nämlich die Wahrscheinlichkeiten für das Auftreten von false-positive- und false-negative-Fehlern, so kann man zu jeder zulässigen Matrix (zulässig bedeutet, dass diese Matrix im fehlerfreien Fall hätte erzeugt werden können) die bedingte Wahrscheinlichkeit dafür berechnen, dass diese Matrix die eigentliche Matrix ist, unter der Bedingung der tatsächlich beobachteten Hybridisierungsmatrix. Optimierungsproblem Man möchte diejenige Matrix finden, für die diese Wahrscheinlichkeit maximal ist. Dazu muss man ein sogenanntes kombinatorisches Optimierungsproblem lösen. In diesem Fall ein gewichtetes Consecutive Ones Problem. Branch-and-Cut Dieses Optimierungsproblem lösen wir mit dem sogenannten Branch-and-Cut Ansatz. Dabei wird ein Polytop konstruiert, dessen Ecken zu den zulässigen Lösungen des Problems gehören. Gesucht wird dann die optimale Ecke im Polytop. Der Branch-and-Cut Ansatz bietet den großen Vorteil, dass man damit nicht nur sehr gute Lösungen finden kann, sondern auch zu jeder Zeit in der Optimierungsphase eine Abschätzung erhält, wie weit die bis dahin beste Lösung höchstens vom Optimum entfernt ist.

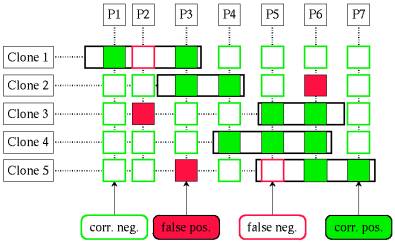
Abb. 1: Dieses Bild zeigt eine Hybridisierungsmatrix für das Physical Mapping Problem ohne End-Probes. Ausgefüllte Quadrate zeigen eine Hybridisierung an, entsprechend zeigen nicht ausgefüllte Quadrate an, dass das Probe nicht mit dem entsprechenden Clone hybridisiert hat. Weiter sind fehlerhafte Einträge (false-positives und false-negatives) rot und korrekte Einträge grün dargestellt. In diesem Fall kann man der Zeichnung leicht die korrekte Anordnung der Probes und damit auch der Clones entnehmen, man beachte aber, dass die Information, welche Einträge fehlerbehaftet sind und welche nicht, in der Praxis nicht vorliegt. 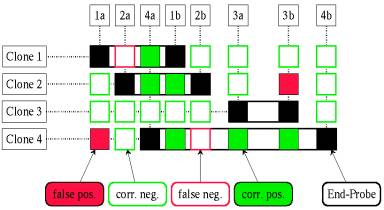Abb. 2: Hier nun eine Hybridisierungsmatrix für das Physical Mapping Problem mit End-Probes. Der Unterschied besteht darin, dass hier die Probes von DNA-Sequenzen aus den Enden der Clones gewonnen werden. Ein Hybridisierungstest zwischen Clone und den beiden zugehörigen End-Probes ist daher nicht notwendig (entsprechenden Quadrate sind schwarz dargestellt), da die relative Lage in beiden Fällen bereits bekannt ist. Ansprechpartner Marcus Oswald Im Neuenheimer Feld 368 69120 Heidelberg Telefon: 06221/54-5746 Email: Marcus.Oswald@informatik.uni-heidelberg.de